二叉查找树
二叉查找树,Binary Search Tree[BST],也称有序二叉树(ordered binary tree),排序二叉树(sorted binary tree),是指一棵空树或具有下列性质的二叉树
1.若任意节点的左子树不为空,则左子树上所有节点的值均小于它的根节点的值
2.若任意节点的右子树不为空,则右子树上所有节点的值均大于它的根节点的值
3.任意节点的左右子树也分别是二叉查找树
4.没有键值相等的节点
因为一棵由 n 个节点随机构造的二叉树高度为 lgN,所以一般操作的执行时间为 O(lgN)
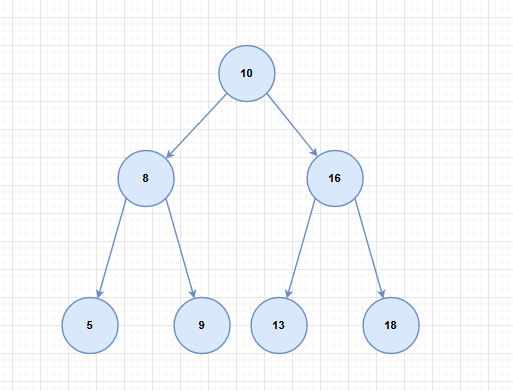
上图,结合二叉查找树的三条约束来看,没有什么问题,下图依旧符合上面三条约束,却是存在问题的
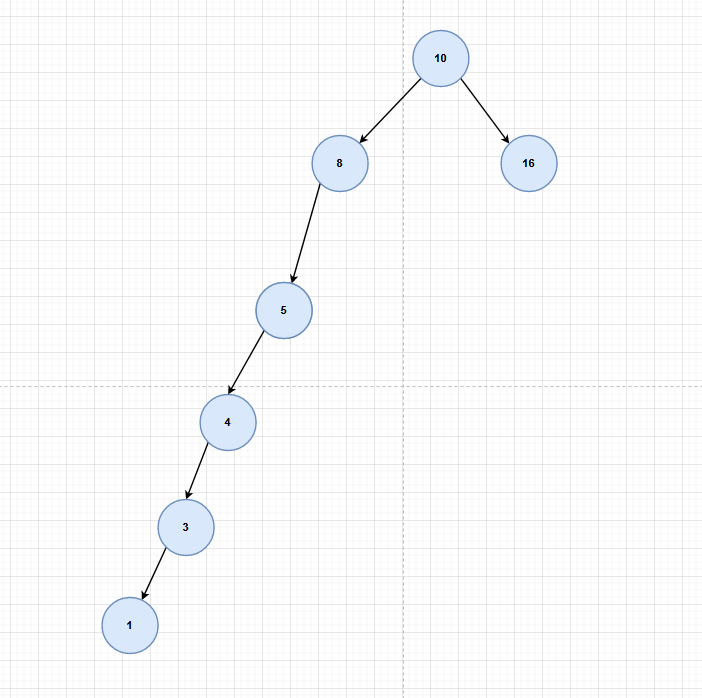
二叉树若退化成了一颗具有 n 个节点的线性链后,操作的最坏时间复杂度为 O(N)
红黑树会通过一些性质使树相对平衡,使得最终查找、插入、删除的时间复杂度最坏情况下依然为 O(lgN)
红黑树
红黑树,Red-Black Tree[RBT],是一个自平衡(不是绝对的平衡)的二叉查找树(BST),树上的每个节点都遵循下面的规则:
1.每个节点要么是红的,要么是黑色
2.根节点是黑色的
3.每个叶子节点(叶子节点即指树尾端 nil 指针或 NULL 节点)是黑色
4.如果一个节点是红色,那么它的两个儿子是黑色
5.对于任一节点而言,其到叶节点的每一条路径都包含相同数目的黑色节点
正是红黑树的这 5 条性质,使得一棵 n 个节点的红黑树始终保持了 lgN 的高度,也就是红黑树查找、插入、删除的最坏时间复杂度为 lgN
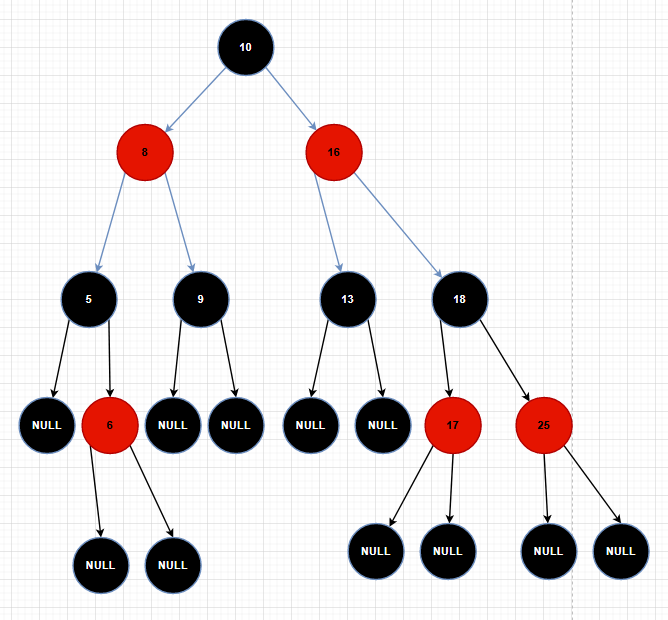
红黑树的旋转与变色
当我们在对红黑树进行插入或删除等操作时,对树的结构进行了修改,可能会违背红黑树的性质
为了继续保持红黑树的性质,我们会进行两种操作:
1.recolor(变色,重新标记红色或黑色)
2.rotation(旋转)
先尝试 recolor,如果 recolor 不能达到红黑树的要求,就尝试 rotation
步骤:
假设新插入的节点为 X
1.将新插入的节点标记为红色
2.如果 X 是根节点(root),则标记为黑色
3.如果 X 不是根节点且 X 的 parent 不是黑色
3.1 如果 X 的 uncle(叔叔)是红色
3.1.1 将 parent 和 uncle 标记为黑色
3.1.2 将 grand parent(祖父)标记为红色
3.1.3 将 G 变成新的 X,然后重复步骤 2、3
3.2 如果 X 的 uncle(叔叔)是黑色,要分成四种情况处理
3.2.1 左左(P 是 G 的左儿子,X 是 P 的左儿子)
3.2.2 左右(P 是 G 的左儿子,X 是 P 的右儿子)
3.2.3 右右(P 是 G 的右儿子,X 是 P 的右儿子)
3.2.4 右左(P 是 G 的右儿子,X 是 P 的左儿子)
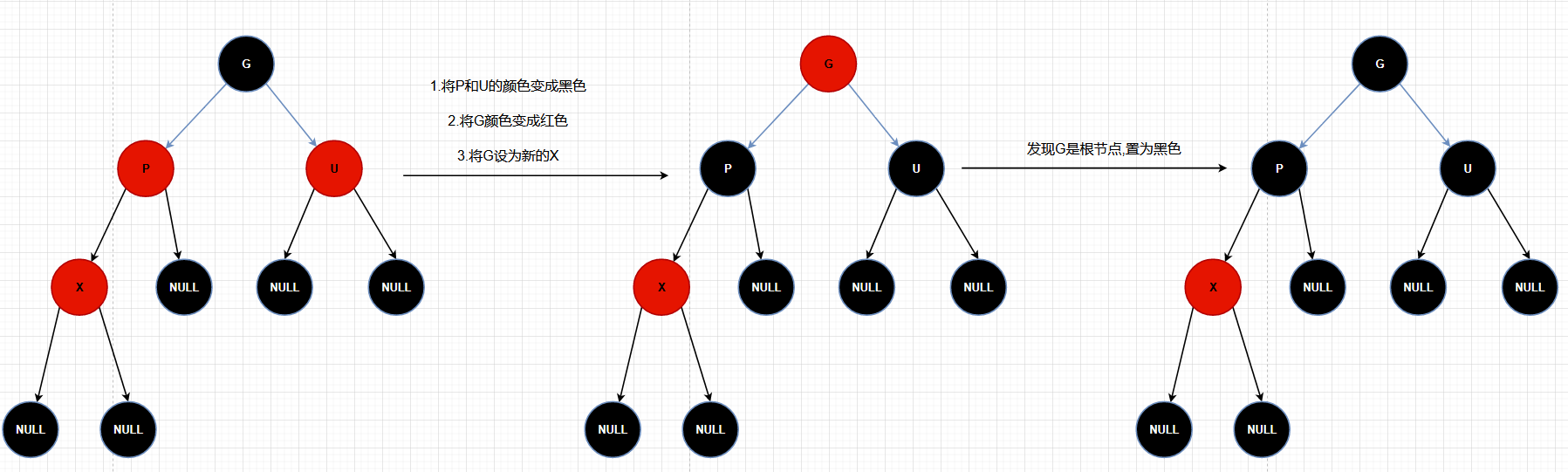
uncle 是红色
1.将新插入的节点 X 标记为红色
2.发现 X 的 parent(P)同样为红色,这违反了红黑树的第三条规则:不能有两个连续相邻的红色节点
3.发现 X 的 uncle(U)同样为红色
4.将 P 和 U 标记为黑色
5.将 X 和 X 的 grand parent (G)标记为相同的颜色,即红色,将 G 设为新的 X,继续重复 2、3
6.发现 G 是根节点,标记为黑色
7.结束
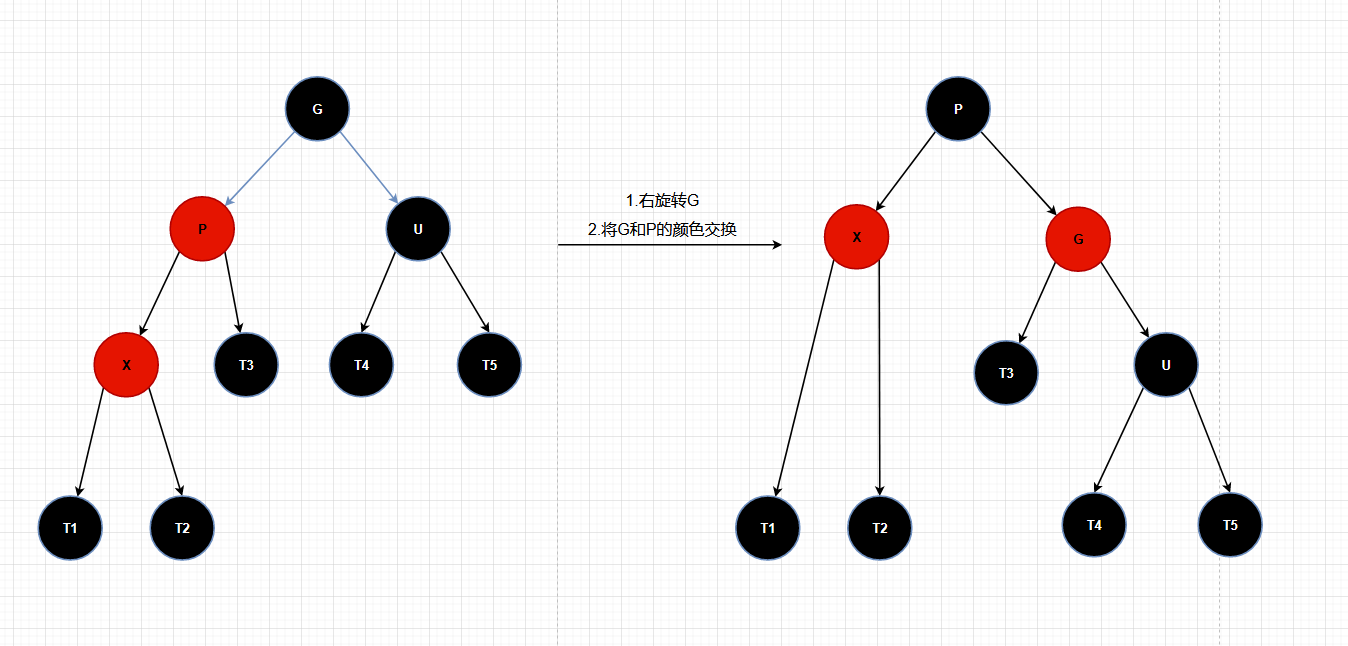
左左
想象这是一根绳子,手提起 P 点,然后变色
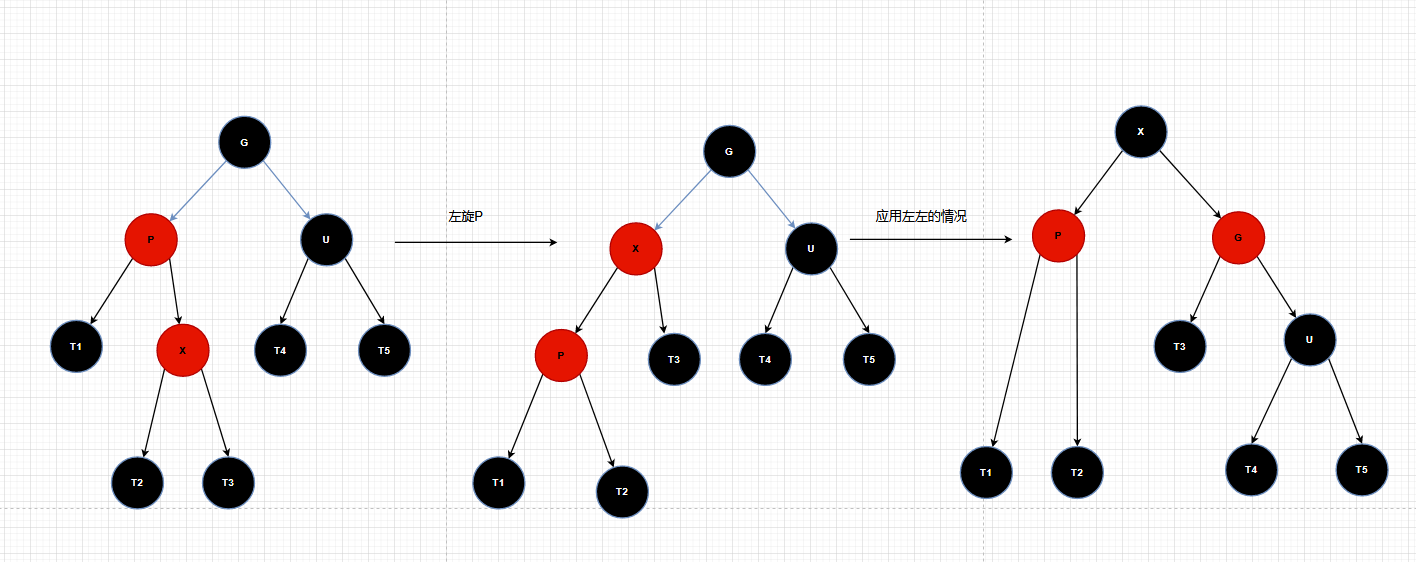
左右
左旋:使 X 的父节点 P 被 X 取代,同时父节点 P 成为 X 的左孩子,然后再应用左左情况
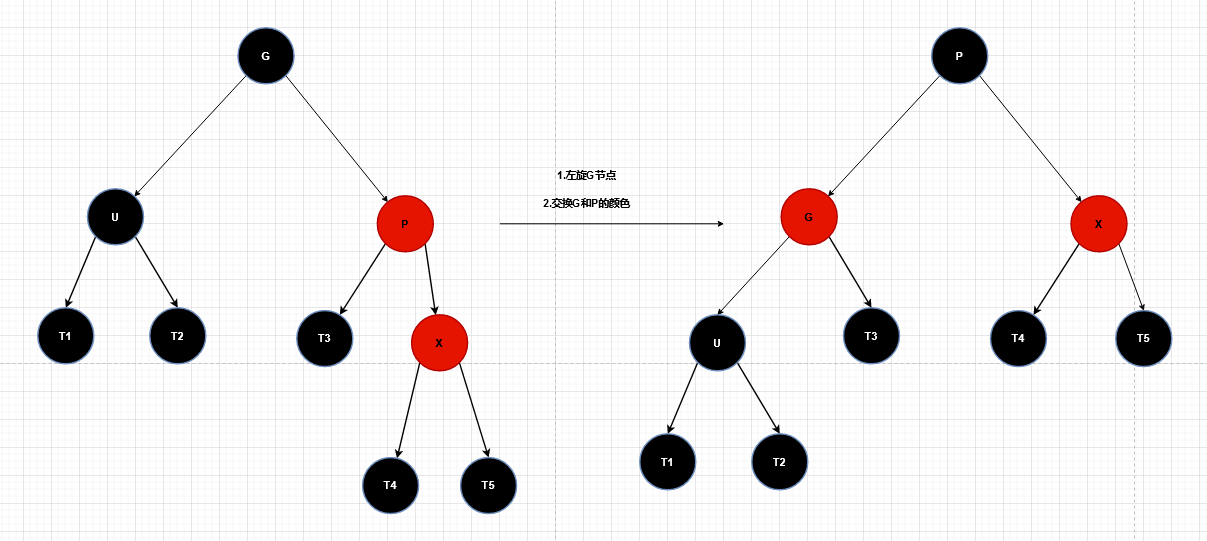
右右
与左左情况一样,想象成一根绳子
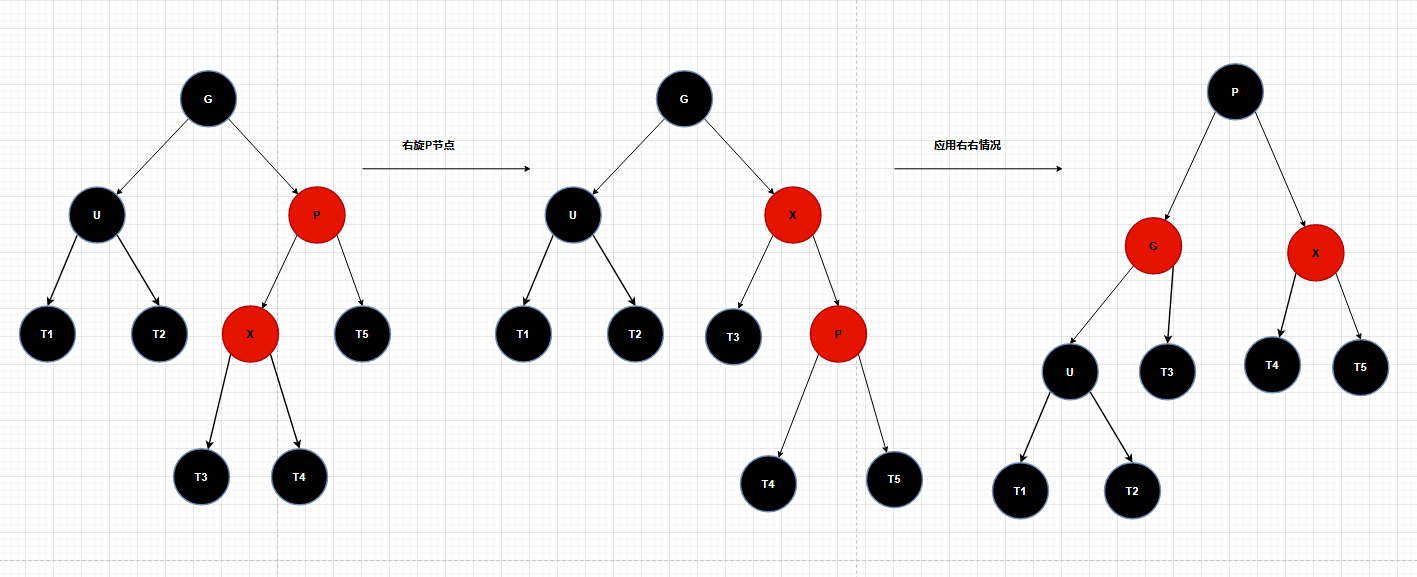
右左
右旋:使 X 的父节点 P 被 X 取代,同时父节点 P 成为 X 的右孩子,然后再应用右右情况